最近都在学习逻辑回归,看了不少博客的文章,有详细的,有直接上来就是贴公式的,很暴力。
不管怎样,还是要感谢博主们贡献出来的文章,也从中收获了不少。
自己学习后,把自己理解的整理归纳下,所以有了这篇文章,希望能帮助到正在学习逻辑回归的同学吧。
如果哪里写的有问题,或者有疑问,请指出留言,感谢。
基本概念
回归是由英国著名生物学家兼统计学家高尔顿(Francis Galton,1822~1911)在研究人类遗传问题时提出来的。为了研究父代与子代身高的关系,高尔顿搜集了1078对父亲及其儿子的身高数据。他发现这些数据的散点图大致呈直线状态,也就是说,总的趋势是父亲的身高增加时,儿子的身高也倾向于增加。但是,高尔顿对试验数据进行了深入的分析,发现了一个很有趣的现象—回归效应。因为当父亲高于平均身高时,他们的儿子身高比他更高的概率要小于比他更矮的概率;父亲矮于平均身高时,他们的儿子身高比他更矮的概率要小于比他更高的概率。它反映了一个规律,即这两种身高父亲的儿子的身高,有向他们父辈的平均身高回归的趋势。对于这个一般结论的解释是:大自然具有一种约束力,使人类身高的分布相对稳定而不产生两极分化,这就是所谓的回归效应。
Logistic Regression,逻辑回归,简称LR,是机器学习领域一种常用的算法或模型,属于Supervised Learning监督学习,是指对已知数据(历史数据等)进行训练,产生一个推断的功能。
LR是一种分类算法。也就是把一个群体分类别,可以是具体的问题,已知的数据等。比如:男人/女人,今天会下雨/今天不会下雨,广告是否点击等。
机器学习的主旨就是通过对历史数据的计算(学习),得到一些未知的参数,从而可以判断出新数据会有什么结论。比如:y = ax + b,以下是已知的几组(x,y)历史数据
| x | y |
|---|---|
| 1 | 5.5 |
| 1.5 | 6.0 |
| 2 | 6.5 |
在已知历史数据的情况下,怎么预测自变量x =3 ,因变量y = ?
求因变量y的问题,就转换为计算出两个未知参数a和b的值,有了这两个值,给定任意一个x,都能通过y = ax + b计算出y的值,这就是预测。
LR差不多也是这样,有一个函数 y = f(X),里面包含了N个未知参数ɵ0,ɵ1,ɵ2,… ɵn。因变量y通常会跟很多自变量x有关系,既x0,x1,x2,…xn,所以自变量是一个向量,用大写X表示。同样的,那一堆未知参数也是一个向量,用字母ɵ来表示。
ɵTx,这是参数向量和自变量向量的点积,表达的含义:计算某个事件发生的可能性,可以把这个事件相关的所有特征加权求和。比如,要求今天下雨的可能性,可以把今天所有和下雨相关的概率加权求和,例如有台风经过权重为6,清明时期权重为9等等其他特征,每一个特征都影响”今天下雨的可能性”,用数学表达式表达:
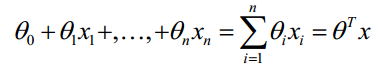
这个加权求和的结果是在(-∞,+∞)范围内的,为了能表示预测的概率,要把输出值在(0,1)之间。所以,逻辑函数就出现了。
逻辑函数
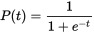
又叫Sigmoid函数
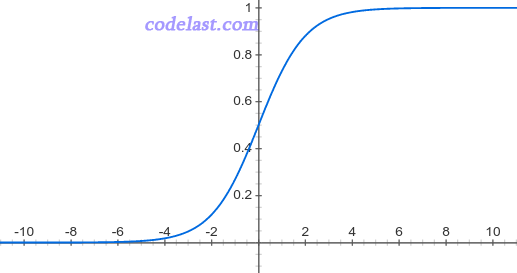
把ɵTx代入到逻辑函数中,就形成了预测函数(hypothesis函数)
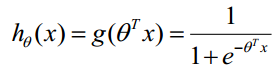
通过逻辑函数,就可以计算出一个事件的概率(0,1)的范围内。但得到了(0,1)之间的任意值并不能进行分类,所以要把这个概率值归类。
f(X) > 0.5的时候,归到类别1中
f(X) <= 0.5的时候,归到类别2中
已经有了预测函数了,那么现在只要求出函数表达式中的未知参数向量ɵ了,求出的参数向量ɵ不是函数的解析解,而是最优解,这是LR最为核心的计算。
损失函数(Loss Function)
损失函数用来衡量预测值与实际值的偏离程度,就是h和y之间的偏差。如果预测完全精确,损失函数值为0;不为0,就表示预测的偏离程度,记为J(ɵ)。
显然,损失函数值越小表示预测函数越正确,使损失函数值最小的那些未知参数ɵ,就是最优的参数值。
损失函数有很多种,0-1损失函数;平方损失函数,用于线性回归;对数损失函数,用于逻辑回归;Hinge损失函数,用于支持向量机(SVM)。
损失函数推导:
y - hɵ(X)
但这是当y=1的时候比较好。如果y=0,则y- hθ(x)= - hθ(x)是负数,不太好比较,则采用其绝对值hθ(x)即可。综合表示如下
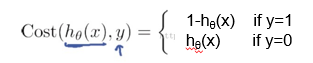
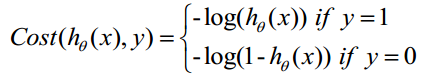
对于输入x分类结果为类别0和类别1的概率:
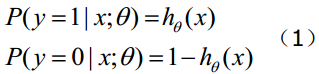
将此表达式综合起来,既y = 1和 y = 0的情况 :
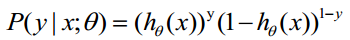
取似然函数 :
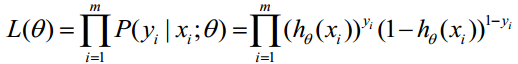
对数似然函数 :
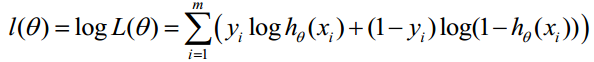
最终J(ɵ)函数 :
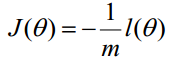
乘了一个负的系数-1/m,所以取J(ɵ)最小值时的ɵ为要求的最佳参数。
把h函数代入 :
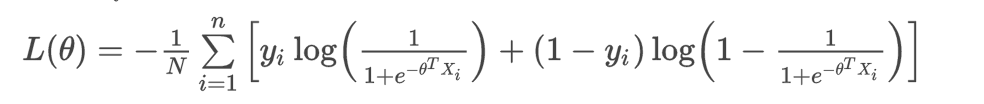
已知 :N为训练数据的条数,有多少组(X,y),N就是多少。
已知 :yi是真实值。
已知 :xi是输入的特征向量
所以整个表达式里只有ɵ是未知的。
只要找到一个未知参数向量ɵ,能使得表达式值最小,这个参数向量ɵ就是最优的参数向量。
求得最优的ɵ之后,代入到预测函数(h函数),对于任意一个未知的X,都可以计算出X所属的分类。
梯度下降
梯度下降求最小值,既为最优的ɵ。对J(ɵ)求偏导
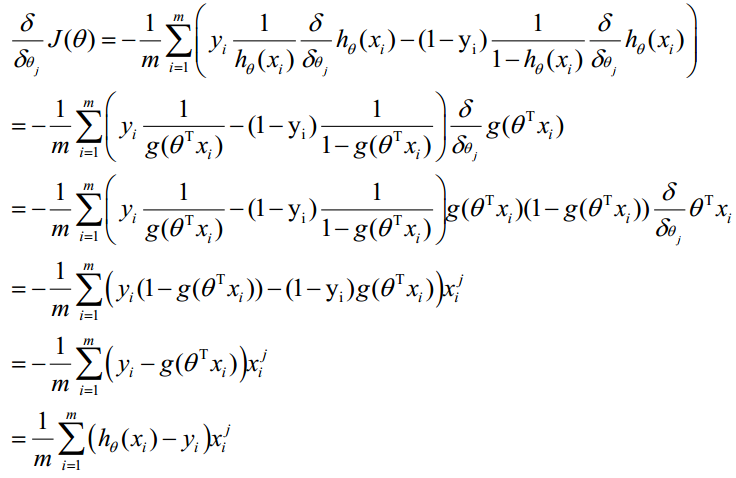
ɵ更新过程 :
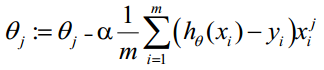
该表达式一直被迭代执行,直到达到某个停止条件为止,比如迭代次数到达某个指定值或达到某个可以允许的误差范围。
a是学习率,又叫步长,初始值。如何正确定义a的值?
学习率过大,随着迭代次数增加,J(ɵ)越来越大,造成无法收敛的情况。
学习率太小,找到最小的J(ɵ)速度就很慢,迭代次数多。
所以要根据实际情况,观察J(ɵ)的值来确定合适的学习率。
梯度上升和梯度下降算法是一样的,表达式中的减法要变加法,上升用来求函数最大值,下降求最小值。
对于LR来说,就是 :
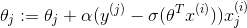
下面是梯度下降的图形:
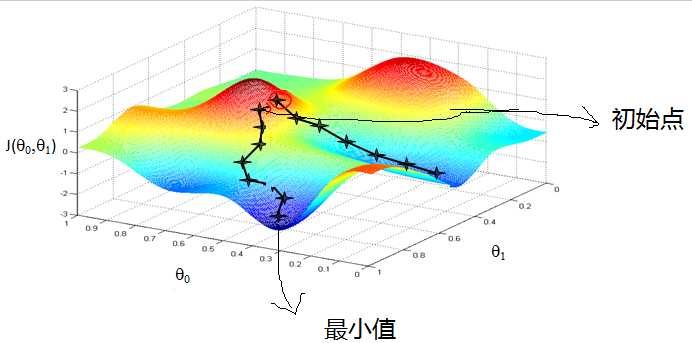
Feature Scaling
翻译特征缩放,应用于梯度下降,为了加快梯度下降的执行速度。
将所有的特征的值标准化,使得取值范围大致都在 -1 <= x <= 1之间。
常用的方法是Mean Normalization,翻译平均标准化。
x - mean(x) / (max - min)
mean(x) 为训练数据特征的平均值,max最大值,min最小值。
Vectorization
Vectorization是使用矩阵计算来代替for循环,简化计算,提高效率。
ɵ更新过程Σ(…)是一个求和的过程,需要使用for语句循环n次。
预定训练数据的矩阵形式如下,x的每一行为一条训练样本,每一列为不同的特征取值。

g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知hɵ(x)-y可由g(A)-y一次计算求得。
θ更新过程可以改为:
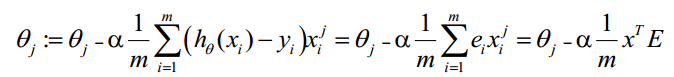
综上所述,Vectorization后θ更新的步骤如下:
-
求 A = X * ɵ
-
求 E = g(A) - y
-
求 ɵ:= ɵ - axTE
正则化Regularization
过拟合问题源自过多的特征。
解决方法是:
-
减少特征数量
-
正则化
正则化后的梯度下降算法θ的更新变为:
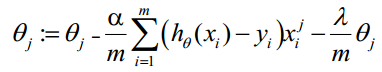
lambda是正则项系数:
-
如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,但是可能出现欠拟合的现象;
-
如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上的偏差会小,但是可能会导致过拟合。